부동 소수점의 의미
영어로 floating point라고 하며, 소수점이 떠다닌다는 의미를 가지고 있습니다.
컴퓨터에서 실수를 표현하는 방법으로 소수점의 위치를 고정하지 않아, 사용하는 비트 수 대비 넓은 범위의 숫자를 표현한다는 장점이 있습니다.
IEEE 754에서 부동 소수점의 개념을 표준화하였습니다.
고정 소수점과의 차이
고정 소수점에서는 정수와 소수 부분의 영역을 나눠서 수를 표현하지만, 부동 소수점에서는 유동적으로 소수점을 이동시킬 수 있습니다.
32비트만큼을 사용해서 실수를 표현한다고 가정할 때, 고정 소수점을 부호 1비트, 정수 부분을 8비트, 소수 부분을 23비트로 표현한다고 합시다. (1+8+23 = 32)
그런데, 정수 부분은 8비트만큼만 사용할 수 있어서 -2^8 ~ 2^8 (-256 ~ 256) 만큼의 정수만 표현할 수가 있습니다.
소수 부분까지 합친다면 -256.xxx ~ 256.xxx 범위의 수를 표현할 수 있는 것인데요.
숫자를 표현하는 범위가 작다는 단점이 있습니다.

부동 소수점 표현
부동 소수점도 32비트로 표현해볼 수 있는데요.
부동 소수점은 1)가수 (fraction), 2)지수 (exponent), 3)밑수 (base) 로 수를 표현할 수 있습니다.
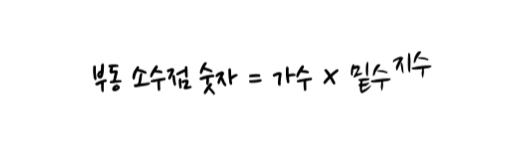

십진수 13.075를 부동 소수점으로 표현하면, 1.3075 * 10^1 또는 0.13075 * 10^2 형태로 표현할 수 있는 것이죠.
13.075를 이진수로 변경하면, 1101.11 가 되고 11.0111 * 2^2 또는 0.110111 * 2^4 처럼 부동 소수점으로 표현할 수 있습니다.
고정 소수점 (32비트 기준) 에서 정수 부분을 8비트로 잡았을 때, 숫자의 범위가 굉장히 제한적이었는데요.
부동 소수점 (32비트 기준)에서는 지수 부분이 8비트라면, 지수의 값의 범위가 0~256 되기 때문에 큰 숫자를 표현할 수 있습니다.
물론 고정 소수점에서 정수 부분의 비트 공간을 늘리고 소수 부분의 비트 공간을 줄여서, 숫자의 크기를 늘릴 수 있습니다.
그럼에도 불구하고, 표현할 수 있는 소수 범위가 좁아지고 부동 소수점에 비해 표현할 수 있는 숫자의 크기에 한계가 있습니다.
부동 소수점의 정규화
부동 소수점에서의 정규화의 의미는,,
가수의 첫 번째 자리가 밑수보다 작은 한 자리 자연수가 되도록 소수점 위치를 이동시키는 것입니다.
2진수에서 부동 소수점을 정규화하면, 가수의 첫 번째 자리 (정수 부분) 는 항상 1이 되는데요.
그렇기에, 이 1을 생략해주고 1비트 만큼의 공간이 생기므로 소수 부분의 숫자를 한 자리 더 넣어줄 수 있습니다.
이진수 1101.11을 정규화된 부동 소수점으로 표현하면 1.10111 * 2^3 이 됩니다.
가수 부분에 첫 번째 1을 생략해서 아래와 같이 표현할 수 있습니다.
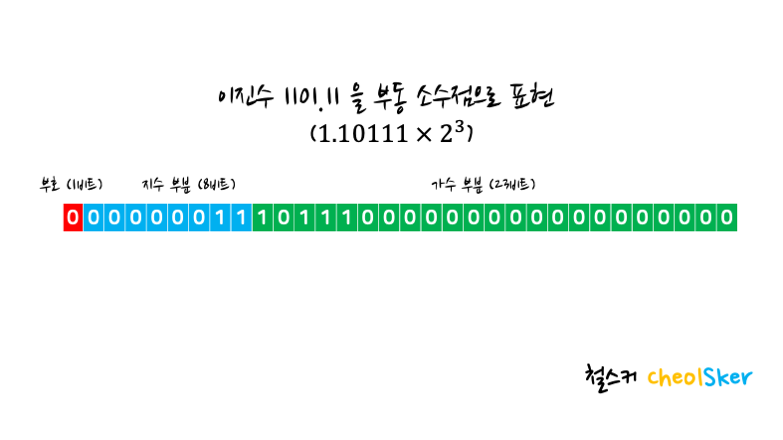
지수의 값은 3이라서 이진수 11을 지수 부분에 넣어줬는데요.
실제로는 이진수 11이 아닌 다른 값이 들어가게 됩니다.
그 부분은 아래에서 추가적으로 설명하겠습니다.
편향된 지수 (biased exponent)
부동 소수점의 지수 부분에는 지수를 위한 부호 비트가 없습니다.
지수가 음수인 경우를 표현을 해줘야 하는데요.
그래서 편향된 지수라는 개념이 등장합니다.
바이어스 (biased) 라는 말처럼 지수를 어느 정도 치우치는 것인데요.
쉽게 말해서, 지수값에 특정값을 더해줘서 지수의 음수값과 지수의 양수값을 표현해주겠다는 것입니다.
지수의 값은 2^(비트 수) 만큼 표현될 수 있는데요. (8비트 기준, 2^8 = 256)
그 범위를 절반을 자르고, 0 한개를 제외한 값을 특정 상수 (바이어스 상수)로 정합니다.
(8비트 기준) (2^8 / 2) - 1 = 127
편향된 지수의 개념은, 지수값이 바이어스 상수인 경우 (여기서는 127) 지수값이 0이라고 생각하는 것입니다.
즉, 기존 지수의 값에 바이어스 상수를 빼주면, 편향된 지수의 값을 알 수 있습니다.

지수 비트가 모두 0이거나 1인 경우는 특별하게 사용되는 데요.
그 이유는 아래에서 얘기해보도록 하겠습니다.
지수 부분의 모든 비트가 0이거나 1인 경우
가수의 첫 번째 값을 1로 생략한다고 했는데, 그럼 숫자 0을 표현할 수 없습니다.
지수값이 아무리 작더라도 가수의 형태가 1.xxxxxx 이기 때문에, 0이 되지 않기 때문입니다.
그래서, 모든 비트가 0인 경우와 1인 경우는 조금 다르게 동작하는 것으로 약속을 하였습니다.
지수 부분의 모든 비트가 0인 경우
1. 생략되는 가수의 첫 번째 정수를 0으로 사용한다.
2. 편향된 지수값은 -127이 아닌 -126을 사용한다.
1-1. 1번의 경우, 모든 비트가 0이면 숫자 0을 표현할 수 있습니다.
생략되는 첫번째 가수의 비트가 0이고, 나머지 가수 부분의 비트도 0이기 때문입니다.
(0.00000 ... * 2^(-126) = 0)
1-2. **2^(-127) 보다 작은 값도 표현할 수 있게 됩니다.**
가수 부분이 23비트로 존재하고, 가장 마지막 가수 부분의 비트가 1이라면,
부동 소수점 정규화 표현으로 1 * 2^(-149) 로 표현 가능한데, 이 값은 2^(-127)보다 매우 작은 값입니다.
지수 부분의 모든 비트가 1인 경우
1. 무한 (infinity)
2. NaN (Not a Number)
1-1. 가수 부분이 모두 0이면, 무한의 값을 나타냅니다.
부호 비트에 따라 -infinity와 infinity를 나타냅니다.
(부호 비트가 1이면 -infinity, 0이면 infinity)
1-2. 가수 부분에 1이 한 개 이상 존재하면, NaN 을 나타냅니다.
위와 마찬가지로 부호 비트에 따라 -Nan과 Nan 값을 나타냅니다.
부동 소수점도 한계가 있다
부동소수점을 32비트 기준으로 설명했지만, 64비트, 128비트 등..
비트 수를 더 늘려서, 실수를 더 정밀하게 표현할 수 있습니다.
그렇지만, 무한소수처럼 부동 소수점의 표현법이나 2진수로 표현할 수 없는 값들도 존재합니다.
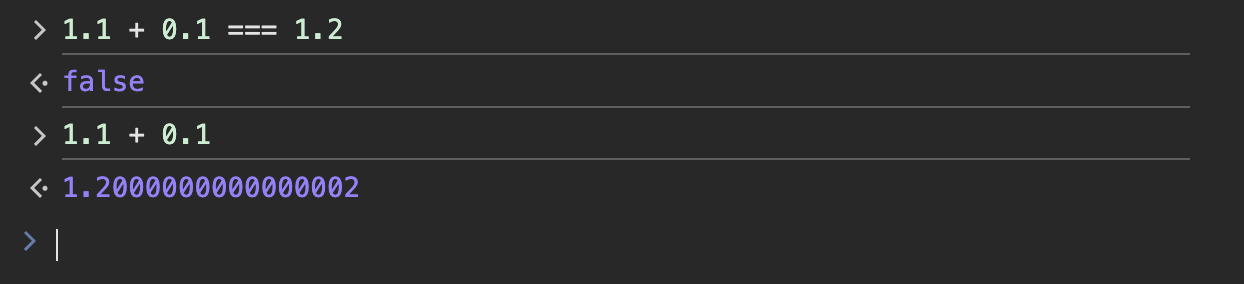
부동 소수점을 잘 정의하여 넓은 범위의 숫자를 표현할 수 있게 되었지만, 모든 숫자를 표현할 수 없다는 점.
특정한 경우에는 값의 오차가 생긴다는 점을 인지하면서, 개발을 진행하시면 좋을 것 같습니다.
참고
